В статье рассмотрим расчеты прочности материалов при механических воздействиях: растяжении, кручении и изгибе. Понимание этих процессов важно для инженеров и проектировщиков, так как позволяет предсказать поведение конструкций под нагрузкой и избежать разрушений. Обсудим методы расчета и практические примеры, что поможет читателям лучше ориентироваться в вопросах прочности и надежности материалов в инженерной практике.
Расчеты на прочность при растяжении (сжатии)
Начнем с основного типа деформации — растяжения и сжатия. Чтобы вычислить напряжение при центральном растяжении (или сжатии), нужно разделить продольную силу на площадь поперечного сечения. Условие прочности записывается так:
где сигма в квадратных скобках обозначает допустимое напряжение, которое определяется делением предельного напряжения на коэффициент запаса прочности.
Предельные значения напряжения различаются для разных материалов. Например, для пластичных материалов, таких как малоуглеродистая сталь (Ст2, Ст3), предельным напряжением является предел текучести, а для хрупких материалов, таких как бетон или чугун, — предел прочности (временное сопротивление). Эти характеристики определяются в ходе испытаний образцов на растяжение или сжатие с помощью специализированных машин, фиксирующих данные в виде диаграмм.
Коэффициент запаса прочности выбирается инженером на основе опыта, назначения детали и области применения. Обычно его значение колеблется от 2 до 6.
Для расчета размеров сечения минимальная площадь поперечного сечения при центральном растяжении (или сжатии) равна отношению продольной силы к допустимому напряжению.
Эксперты в области механики материалов подчеркивают важность расчетов на прочность при различных механических воздействиях, таких как растяжение, кручение и изгиб. Эти методы позволяют определить пределы прочности материалов и их способность выдерживать нагрузки без разрушения. При растяжении, например, критически важно учитывать не только максимальную нагрузку, но и характеристики материала, такие как модуль упругости и предел текучести. Кручение требует анализа распределения напряжений, что особенно актуально для валов и осей. В свою очередь, изгиб может привести к сложным деформациям, требующим применения теории изгиба. Таким образом, комплексный подход к расчетам на прочность обеспечивает надежность конструкций и безопасность эксплуатации.
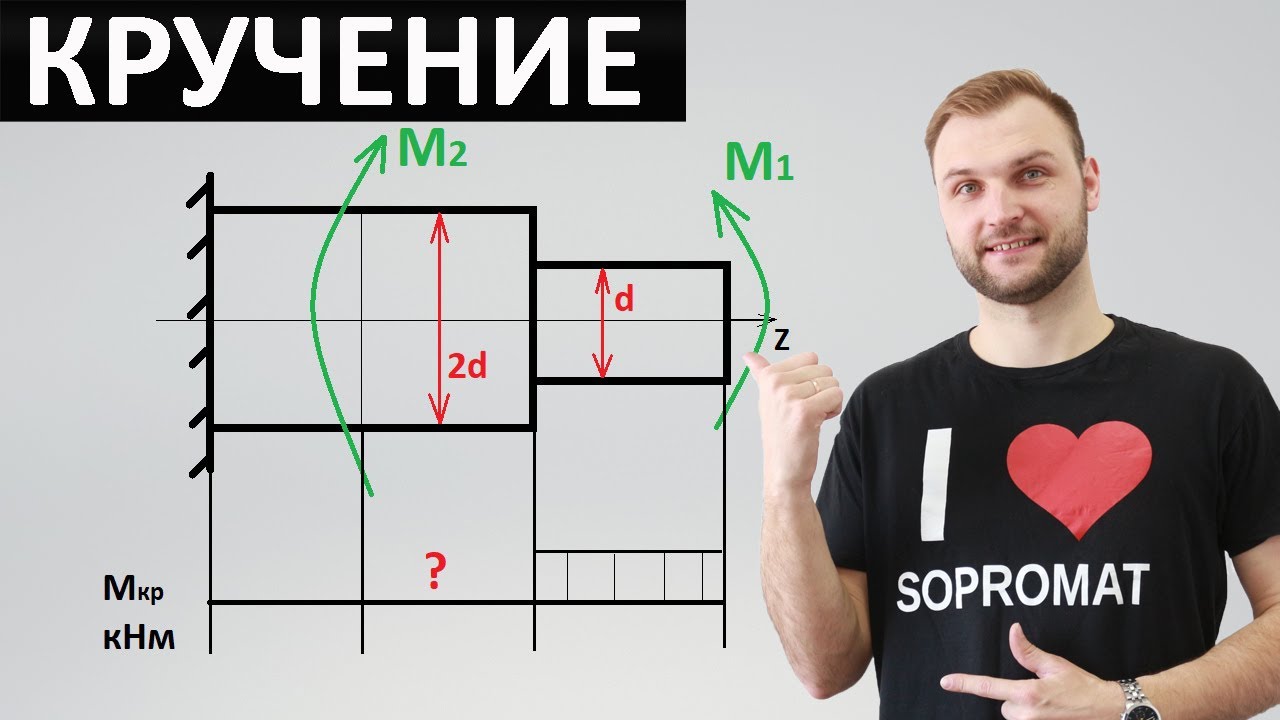
Расчеты на прочность при кручении
При кручении расчеты на прочность в принципе схожи с теми, что проводятся при растяжении. Только здесь вместо нормальных напряжений появляются касательные напряжения.
На кручение работают, чаще всего, детали, которые называются валами. Их назначение заключается в передаче крутящего момента от одного элемента к другому. При этом вал по всей длине имеет круглое поперечное сечение. Условие прочности для круглого поперечного сечения можно записать так:
где Ip — полярный момент сопротивления, ρ — радиус круга. Причем по этой формуле можно определить касательное напряжение в любой точке сечения, варьируя значение ρ. Касательные напряжения распределены неравномерно по сечению, их максимальное значение находится в наиболее удаленных точках сечения:
Условие прочности, можно записать несколько проще, используя такую геометрическую характеристику как момент сопротивления:
То бишь максимальные касательные напряжения равны отношению крутящего момента к полярному моменту сопротивления и должны быть меньше либо равны допустимому напряжению. Геометрические характеристики для круга, упомянутые выше можно найти вот так:
Иногда в задачах встречаются и прямоугольные сечения, для которых момент сопротивления определяется несколько сложнее, но об этом я расскажу в другой статье.
| Тип нагружения | Основная формула для расчета напряжения | Критерий прочности |
|---|---|---|
| Растяжение/Сжатие | σ = F/A | σ ≤ [σ] |
| Кручение | τ = T*r/J | τ ≤ [τ] |
| Изгиб (чистый) | σ = My/I | σ ≤ [σ] |
| Изгиб (с изгибом и растяжением/сжатием) | σ = My/I ± F/A | σ ≤ [σ] |
Интересные факты
Вот несколько интересных фактов, связанных с расчетом на прочность при растяжении, кручении и изгибе:
-
Модуль Юнга и его значение: Модуль Юнга — это мера упругости материала, которая показывает, насколько он деформируется под воздействием растягивающей силы. Например, сталь имеет значительно больший модуль Юнга, чем резина, что делает её более устойчивой к растяжению. Это свойство позволяет инженерам выбирать материалы в зависимости от требований к прочности и жесткости конструкции.
-
Кручение и его применение: При кручении, например, валов и осей, важно учитывать не только прочность материала, но и его геометрию. Увеличение диаметра вала значительно повышает его сопротивляемость кручению. Это объясняет, почему в механических конструкциях часто используются валы с увеличенным сечением в местах, где ожидаются большие нагрузки.
-
Изгиб и критическая нагрузка: При изгибе длинных элементов, таких как балки, важно учитывать не только прочность материала, но и его длину. Существует критическая нагрузка, при превышении которой элемент может потерять устойчивость и прогнуться. Это явление называется «боковым изгибом» и особенно актуально для тонких и длинных конструкций, таких как мосты и строительные балки. Инженеры используют специальные формулы для расчета предельных значений нагрузки, чтобы избежать разрушения конструкции.

Расчеты на прочность при изгибе
Техническая механика
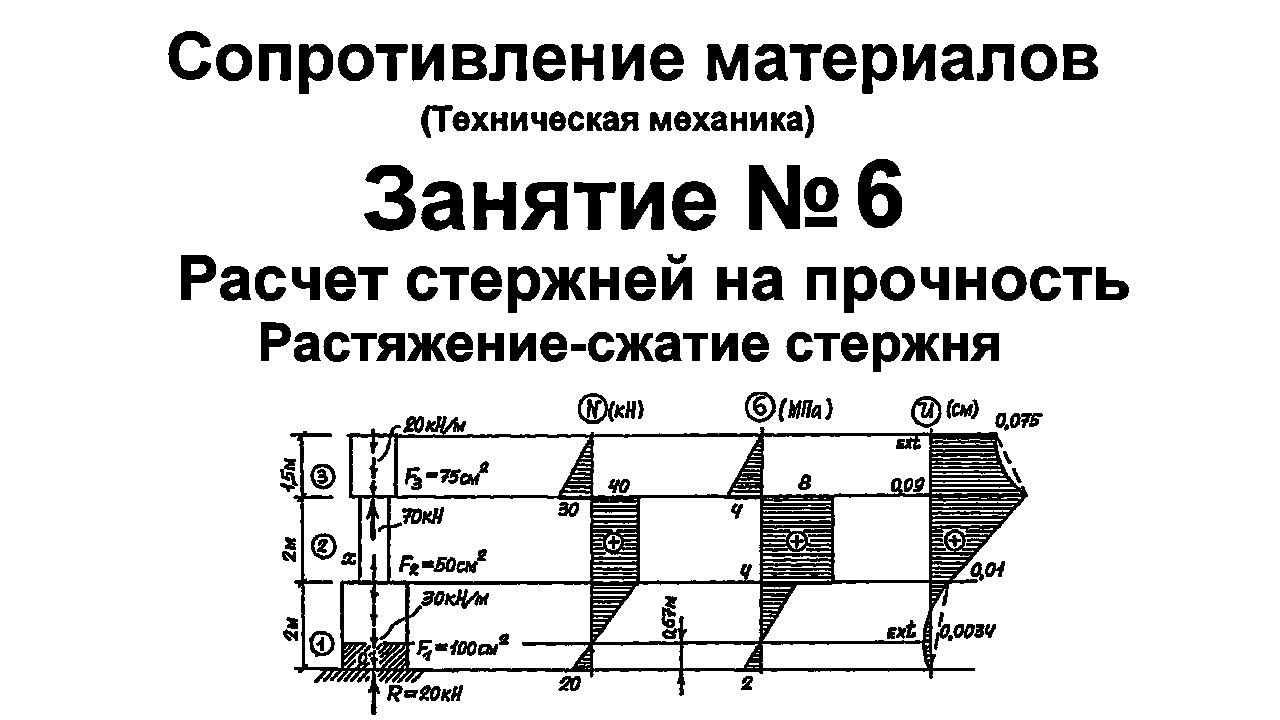
Сопротивление материалов
Решение задач на растяжение и сжатие
Расчеты на прочность при растяжении и сжатии
В механических испытаниях устанавливаются предельные напряжения, при которых происходит сбой или разрушение конструктивных элементов. Для пластичных материалов это предел текучести, а для хрупких — предел прочности.
Чтобы обеспечить прочность деталей, максимальные напряжения в эксплуатации должны оставаться ниже предельных значений. Соотношение между предельным напряжением и рабочим напряжением называется коэффициентом запаса прочности (s):
s = σпред / σ,
где σ = N / A — реальное напряжение в элементе конструкции.
Недостаточный коэффициент запаса прочности может привести к утрате работоспособности конструкции, а слишком высокий — к перерасходу материалов и увеличению веса. Минимально необходимый коэффициент запаса прочности называется допускаемым и обозначается [s].
Соотношение предельного напряжения к допускаемому запасу прочности называется допускаемым напряжением ([σ]):
[σ] = σпред / [s].
Условие прочности для деталей и конструкций заключается в том, что максимальное рабочее напряжение не должно превышать допускаемое:
σmax ≤ [σ], или в альтернативной форме: s ≥ [s].
Если допускаемые напряжения при растяжении и сжатии различаются, их обозначают как [σр] и [σс]. Формула для расчетов при растяжении и сжатии:
σ = N / A ≤ [σ],
означает, что нормальное напряжение в критическом сечении не должно превышать допустимое значение.
На практике расчеты прочности выполняются для следующих задач:
— проектный расчет для определения минимальных размеров критического сечения;
— проверочный расчет для вычисления рабочего напряжения и его сравнения с предельно допустимым;
— определение максимально допустимой нагрузки при заданных размерах критического сечения.
Растяжение под действием собственного веса
Если ось бруса вертикальна, то его собственный вес вызывает деформацию растяжения или сжатия.
Рассмотрим брус постоянного сечения весом G, длиной l, закрепленный верхним концом и нагруженный только собственным весом G (рис.1).
Для определения напряжений в поперечном сечении на переменном расстоянии z от нижнего конца применим метод сечений.
Рассмотрим равновесие нижней части бруса и составим уравнение равновесия:
Σ Z = 0; Nz — Gz = 0, откуда:
Nz = Gz = γ А z,
где γ — удельный вес материала бруса, А — площадь его поперечного сечения, z — длина части бруса от свободного конца до рассматриваемого сечения.
Напряжения, возникающие в сечениях бруса, нагруженного собственным весом, определяются по формуле:
σz = Nz / А = γ А z / А = γ z,
т. е. для нагруженного собственным весом бруса нормальное напряжение не зависит от площади поперечного сечения. Очевидно, что опасное сечение будет находиться в заделке:
σmax = γ l.
Эпюра распределения напряжений вдоль оси бруса представляет собой треугольник.
Если требуется определить максимальную длину бруса, нагруженного собственным весом, используют расчет по предельному допустимому напряжению в сечении:
lпр = [σ] / γ.
Статически неопределимые задачи
В процессе проектирования конструкций возникает необходимость определения неизвестных силовых факторов, таких как реакции связей или внутренние силы. Количество этих неизвестных может превышать число уравнений равновесия, что делает невозможным использование стандартных методов расчета. Задачи, в которых внутренние силовые факторы не определяются только уравнениями равновесия, называются статически неопределимыми. Это часто происходит при анализе конструкций, подверженных температурным деформациям.
Для решения таких задач, помимо уравнений равновесия, необходимо составить уравнение перемещений или деформаций. Рассмотрим невесомый стержень с постоянным сечением площадью A и длиной l, жестко зафиксированный на обоих концах. При нагреве в стержне возникают температурные напряжения сжатия, и мы определим их величину.
Сначала составим уравнение равновесия для стержня: Σ Z = 0; RС — RВ = 0. Это указывает на равенство реакций RС и RВ. Применив метод сечений, установим, что продольная сила N в сечениях стержня равна этим реакциям: N = RС = RВ.
Теперь составим дополнительное уравнение, мысленно убрав правую заделку и заменив ее реакцией RВ. Получаем уравнение деформации: Δlt = ΔlСВ, что означает, что температурное удлинение стержня равно его укорочению под действием реакции RВ, поскольку связи считаются жесткими.
Температурное удлинение стержня вычисляется по формуле: Δlt = αtl, где α — коэффициент линейного расширения материала. Укорочение стержня под действием реакции определяется как: ΔlСВ = RВ l / (EА). Приравняв правые части этих уравнений, получаем: αtl = RВ l / (EА), откуда следует, что RВ = αtEА.
Температурные напряжения в конструкциях могут достигать значительных значений. Чтобы минимизировать их негативное влияние на прочность, применяются различные методы. Например, мосты фиксируются только с одной стороны, оставляя второй конец подвижным. В длинных трубопроводах создаются компенсирующие карманы, петли и другие элементы.
Внутренние усилия при растяжении-сжатии.
Осевое (центральное) растяжение или сжатие прямого бруса вызывается внешними силами, вектор равнодействующей которых совпадает с осью бруса. При растяжении или сжатии в поперечных сечениях бруса возникают только продольные силы N. Продольная сила N в некотором сечении равна алгебраической сумме проекции на ось стержня всех внешних сил, действующих по одну сторону от рассматриваемого сечения. По правилу знаков продольной силы N принято считать, что от растягивающих внешних нагрузок возникают положительные продольные силы N, а от сжимающих — продольные силы N отрицательны (рис. 5).
Чтобы выявить участки стержня или его сечения, где продольная сила имеет наибольшее значение, строят эпюру продольных сил, применяя метод сечений, подробно рассмотренный в статье:
Анализ внутренних силовых факторов в статистически определимых системах
Напряжения при растяжении-сжатии.
Определенная методом сечений продольная сила N — это равнодействующая внутренних усилий, распределенных по поперечному сечению стержня (см. рис. 2, б). Согласно формуле (1), для продольной силы можно записать:
где σ — нормальное напряжение в произвольной точке поперечного сечения стержня.
Для вычисления нормальных напряжений в любой точке бруса необходимо знать их распределение по поперечному сечению. Экспериментальные исследования показывают, что при приложении внешней растягивающей нагрузки поперечные линии, проведенные на поверхности стержня, сохраняют параллельность и не искривляются (см. рис. 6, а). Это явление описывается гипотезой плоских сечений (гипотеза Бернулли): сечения, которые были плоскими до деформации, остаются плоскими и после нее.
Все продольные волокна стержня деформируются одинаково, поэтому напряжения в поперечном сечении равны. Эпюра напряжений σ по высоте поперечного сечения стержня представлена на рис. 6, б. Напряжения равномерно распределены по сечению, то есть во всех точках сечения σ = const. Формула для вычисления величины напряжения выглядит следующим образом:
Таким образом, нормальные напряжения в поперечных сечениях растянутого или сжатого бруса равны отношению продольной силы к площади поперечного сечения. Нормальные напряжения считаются положительными при растяжении и отрицательными при сжатии.
Деформации при растяжении-сжатии.
Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l
Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:
При растяжении продольная деформация положительна, а при сжатии — отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:
где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).
Таблица 1
Модуль продольной упругости для различных материалов
Абсолютная поперечная деформация бруса равна разности размеров поперечного сечения после и до деформации:
Соответственно, относительную поперечную деформацию определяют по формуле:
При растяжении размеры поперечного сечения бруса уменьшаются, и ε’ имеет отрицательное значение. Опытом установлено, что в пределах действия закона Гука при растяжении бруса поперечная деформация прямо пропорциональна продольной. Отношение поперечной деформации ε’ к продольной деформации ε называется коэффициентом поперечной деформации, или коэффициентом Пуассона μ:
Экспериментально установлено, что на упругой стадии нагружения любого материала значение μ = const и для различных материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5 (табл. 2).
Таблица 2
Коэффициент Пуассона.
Абсолютное удлинение стержня Δl прямо пропорционально продольной силе N:
Данной формулой можно пользоваться для вычисления абсолютного удлинения участка стержня длиной l при условии, что в пределах этого участка значение продольной силы постоянно. В случае, когда продольная сила N изменяется в пределах участка стержня, Δl определяют интегрированием в пределах этого участка:
Произведение (Е·А) называют жесткостью сечения стержня при растяжении (сжатии).
Механические свойства материалов.
Ключевыми механическими характеристиками материалов при деформации являются прочность, пластичность, хрупкость, упругость и твердость.
Прочность — способность материала противостоять внешним нагрузкам без разрушения и остаточных деформаций.
Пластичность — свойство материала сохранять значительные остаточные деформации без разрушения. Остаточные деформации возникают после снятия нагрузок.
Хрупкость — характеристика, при которой материал разрушается при небольших остаточных деформациях (например, чугун, бетон, стекло).
Идеальная упругость — способность материала полностью восстанавливать форму и размеры после устранения причин деформации.
Твердость — свойство материала сопротивляться проникновению других тел.
Теперь рассмотрим диаграмму растяжения стержня из малоуглеродистой стали. Предположим, что круглый стержень длиной l0 и с постоянным поперечным сечением A0 подвергается статическому растяжению с обоих концов силой F.
Диаграмма сжатия стержня представлена на рисунке (рис. 10, а), где Δl = l — l0 обозначает абсолютное удлинение; ε = Δl / l0 — относительное продольное удлинение; σ = F / A0 — нормальное напряжение; E — модуль Юнга; σп — предел пропорциональности; σуп — предел упругости; σт — предел текучести; σв — предел прочности; εост — остаточная деформация после снятия нагрузок. Для материалов без четкой площадки текучести вводится условный предел текучести σ0,2 — напряжение, при котором достигается 0,2% остаточной деформации. При достижении предела прочности в центре стержня происходит локальное утончение диаметра, образующее «шейку». Дальнейшее удлинение происходит в области шейки (зона местной текучести). Когда напряжение достигает предела текучести σт, поверхность стержня становится матовой — появляются микротрещины (линии Людерса-Чернова), направленные под углом 45° к оси стержня.
Расчеты на прочность и жесткость при растяжении и сжатии.
Опасным сечением при растяжении и сжатии называется поперечное сечение бруса, в котором возникает максимальное нормальное напряжение. Допускаемые напряжения вычисляются по формуле:
где σпред — предельное напряжение (σпред = σт — для пластических материалов и σпред = σв — для хрупких материалов); [n] — коэффициент запаса прочности. Для пластических материалов [n] = [nт] = 1,2 … 2,5; для хрупких материалов [n] = [nв] = 2 … 5, а для древесины [n] = 8 ÷ 12.
Расчеты на прочность при растяжении и сжатии.
Основная задача расчета конструкции — определить ее эксплуатационную пригодность при минимальных затратах материалов. Это достигается через методы оценки прочности и жесткости.
Методы экспериментального определения прочности материалов
Определение прочности материалов является ключевым этапом в инженерной практике, так как оно позволяет оценить, как материалы будут вести себя под воздействием различных нагрузок. Существует несколько методов экспериментального определения прочности, каждый из которых имеет свои особенности и области применения.
1. Испытания на растяжение
Испытания на растяжение являются одним из наиболее распространенных методов для определения прочности материалов. В ходе этого испытания образец материала, обычно в форме цилиндра или пластины, подвергается растягивающей нагрузке до момента разрушения. Основные параметры, которые определяются в результате испытания, включают:
- Предельная прочность: максимальная нагрузка, которую материал может выдержать перед разрушением.
- Удлинение: относительное изменение длины образца, которое происходит до разрушения.
- Модуль упругости: отношение напряжения к деформации в упругой области.
Испытания на растяжение позволяют не только определить прочность, но и оценить пластичность и хрупкость материала, что является важным для выбора материала в зависимости от условий эксплуатации.
2. Испытания на кручение
Испытания на кручение используются для определения прочности материалов на сдвиг. В этом методе образец подвергается крутящему моменту, что приводит к его деформации. Основные характеристики, которые определяются в ходе испытаний на кручение, включают:
- Предельный крутящий момент: максимальный момент, который материал может выдержать до разрушения.
- Угол кручения: угол, на который образец закручивается до момента разрушения.
- Модуль сдвига: отношение сдвигового напряжения к углу сдвига в упругой области.
Данный метод особенно важен для материалов, которые будут подвергаться вращающимся нагрузкам, например, в валках, шестернях и других механизмах.
3. Испытания на изгиб
Испытания на изгиб позволяют оценить прочность материалов на изгиб, что особенно актуально для конструкций, которые будут подвергаться изгибающим нагрузкам, таких как балки и плиты. В процессе испытания образец помещается на опоры и нагружается в центральной части. Основные параметры, которые определяются в ходе испытания, включают:
- Предельная изгибная прочность: максимальная нагрузка, которую материал может выдержать до разрушения при изгибе.
- Модуль изгиба: отношение изгибного напряжения к изгибной деформации в упругой области.
- Максимальное отклонение: величина прогиба образца под действием нагрузки.
Испытания на изгиб позволяют не только определить прочность, но и оценить жесткость материала, что важно для проектирования конструкций, которые должны выдерживать определенные нагрузки без значительных деформаций.
4. Выбор метода испытаний
Выбор метода испытаний зависит от типа материала, условий его эксплуатации и требований к прочности. Например, для металлических конструкций часто используются испытания на растяжение и кручение, в то время как для бетонных и деревянных конструкций более актуальны испытания на изгиб. Важно также учитывать, что результаты испытаний могут варьироваться в зависимости от условий, таких как температура, влажность и скорость нагружения.
Таким образом, экспериментальное определение прочности материалов является важным этапом в инженерной практике, позволяющим обеспечить надежность и безопасность конструкций. Правильный выбор метода испытаний и тщательный анализ полученных данных позволяют инженерам принимать обоснованные решения при проектировании и эксплуатации различных объектов.
Вопрос-ответ
Как рассчитать прочность при растяжении?
Для расчета прочности при растяжении необходимо определить максимальную нагрузку, которую материал может выдержать до разрушения, и разделить её на площадь поперечного сечения образца. Формула выглядит так: σ = F / A, где σ — прочность при растяжении (в МПа или Н/мм²), F — максимальная сила (в Н), а A — площадь поперечного сечения (в мм²). Также важно учитывать характеристики материала, такие как предел текучести и модуль упругости.
Как рассчитать прочность на растяжение?
Формула прочности на разрыв: S = P/A. Эта формула определяет максимальное напряжение, которое может выдержать материал при растяжении или разрыве до разрыва. Например, предел прочности стали на разрыв обычно составляет от 36 000 до 50 000 фунтов на квадратный дюйм, но может достигать 58 000–70 000 фунтов на квадратный дюйм.
Как рассчитать прочность на изгиб?
Расчет балки на прочность при плоском изгибе. Как и в общем случае, необходимо определить максимальный изгибающий момент, максимальное напряжение и сравнить его с допускаемым напряжением. Для расчета применяются те же формулы: σ = M * y / I и условие прочности σ ≤ [σ].
Как рассчитать коэффициент прочности на изгиб?
Момент сопротивления сечения для обоих соединений рассчитывается по формуле Z = π × (OD^4 — ID^4) / 32 × OD. При этом используются предварительно рассчитанные значения: момент сопротивления сечения коробки (Zbox) = 500 дюйм³, момент сопротивления сечения штифта (Zpin) = 250 дюйм³. Коэффициент прочности на изгиб (BSR) рассчитывается по формуле: BSR = Zbox / Zpin = 2.0.
Советы
СОВЕТ №1
Перед началом расчетов на прочность убедитесь, что вы правильно определили тип нагрузки (растяжение, кручение или изгиб). Это поможет выбрать соответствующие формулы и методы анализа, а также избежать ошибок в расчетах.
СОВЕТ №2
Используйте материалы с известными механическими свойствами. При выборе материала для конструкции обязательно ознакомьтесь с его пределами прочности, модулем упругости и другими характеристиками, чтобы обеспечить надежность и долговечность изделия.
СОВЕТ №3
Не забывайте о факторах безопасности. При проведении расчетов учитывайте коэффициенты запаса прочности, чтобы гарантировать, что конструкция сможет выдерживать нагрузки, превышающие расчетные значения, и избежать потенциальных аварий.
СОВЕТ №4
Проводите экспериментальные проверки. Если это возможно, создайте прототип вашей конструкции и проведите испытания на прочность. Это поможет выявить слабые места и скорректировать проект до его окончательной реализации.